线性表 | HALO

【考纲内容】

线性表的定义和基本操作
线性表的实现（顺序储存；链式储存；线性表的应用）

【知识框架】

线性表

【复习提示】

线性表是考研命题的重点。这类算法题实现起来比较容易而且代码量较少，但却要求具有最优的性能（时间、空间复杂度），才能获得满分。因此，应牢固掌握线性表的各种基本操作（基于两种存储结构），在平时的学习中多注重培养动手能力。另外，需要提醒的是，算法最重要的是思想！考场上的时间有限，在试卷上不一定要求代码具有实际的可执行性，因此应尽力表达出算法的思想和步骤，而不必过于拘泥每个细节。注意算法题只能用C/C++语言实现。

线性表的定义和基本操作

线性表的定义

线性表是具有相同数据类型的 $n \ (n≥0)$ 个数据元素的有限序列，其中 $n$ 为表长，当 $n=0$ 时线性表是一个空表。若用 $L$ 命名线性表，则其一般表示为：$$L=(a_1,a_2,\cdots ,a_i,a_{i+1},\cdots ,a_n)$$ 式中，$a_1$ 是唯一的“第一个”数据元素，又称表头元素；$a_n$ 是唯一的“最后一个”数据元素，又称表尾元素。

除第一个元素外，每个元素有且仅有一个直接前驱。
除最后一个元素外，每个元素有且仅有一个直接后继。

以上就是线性表的逻辑特性，这种线性有序的逻辑结构正是线性表名字的由来。线性表的特点如下：

表中元素的个数有限
表中元素具有逻辑上的顺序性，表中元素有其先后次序
表中元素都是数据元素，每个元素都是单个元素
表中元素的数据类型都相同，这意味着每个元素占有相同大小的存储空间
表中元素具有抽象性，即仅讨论元素间的逻辑关系，而不考虑元素究竟表示什么内容。

注意：线性表是一种逻辑结构，表示元素之间一对一的相邻关系。顺序表和链表是指存储结构，两者属于不同层面的概念，因此不要将其混淆。

线性表的基本操作

一个数据结构的基本操作是指其最核心、最基本的操作。其他较复杂的操作可通过调用其基本操作来实现。线性表的主要操作如下：

InitList(&L)：初始化表。构造一个空的线性表。
Length(L)：求表长。返回线性表 L 的长度，即 L 中数据元素的个数。
LocateElem(L,e)：按值查找操作。在表 L 中查找具有给定关键字值的元素。
GetElem(L,i)：按位查找操作。获取表 L 中第 i 个位置的元素的值。
ListInsert(&L,i,e)：插入操作。在表 L 中的第 i 个位置上插入指定元素 e 。
ListDelete(&L,i,&e)：删除操作。删除表 L 中第 i 个位置的元素，并用 e 返回删除元素的值。
PrintList(L)：输出操作。按前后顺序输出线性表 L 的所有元素值。
Empty(L)：判空操作。若 L 为空表，则返回 true，否则返回 false。
DestroyList(&L)：销毁操作。销毁线性表，并释放线性表 L 所占用的内存空间。

线性表的顺序表示

顺序表的定义

线性表的顺序存储又称顺序表。它是用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。第1个元素存储在线性表的起始位置，第 $i$ 个元素的存储位置后面紧接着存储的是第 $i+1$ 个元素，称 $i$ 为元素 $a_i$ 在线性表中的位序。因此，顺序表的特点是表中元素的逻辑顺序与其物理顺序相同。

假设线性表 L 储存的起始位置为 LOC(A)，sizeof(ElemType) 是每个数据元素所占用储存空间的大小，则表 L 所对应的顺序存储如下图所示。

线性表的顺序存储结构

注意：线性表中元素的位序是从 1 开始的，而数组中元素的下标是从 0 开始的。

顺序表的实现方式

静态分配

假定线性表的元素类型为 ElemType（以下具体操作使用int类型），则线性表的顺序存储类型描述为：

#define MaxSize 10             // 定义线性表的最大长度
typedef struct{
    ElemType data[MaxSize];    // 顺序表的元素
    int length;                // 顺序表的当前长度
} StaticSqList;                // 顺序表的类型定义 Sq:sequence

一维数组可以是静态分配的，也可以是动态分配的。在静态分配时，由于数组的大小和空间事先已经固定，一旦空间占满，再加入新的数据将会产生溢出，进而导致程序崩溃。

// 初始化一个顺序表
void InitList(StaticSqList &L) {
    for (int i = 0; i < MaxSize; i++) {
        L.data[i] = 0;  // 将所有数据元素设置默认值(可省略)
    }
    L.length = 0;       // 顺序表初始长度为0
}

int main(){
    StaticSqList L;     // 声明一个顺序表
    InitList(L);        // 初始化顺序表
    // ...  相关操作
    return 0;
}

动态分配

而在动态分配时，存储数组的空间是在程序执行过程中通过动态存储分配语句分配的，一旦数据空间占满，就另外开辟一块更大的存储空间，用以替换原来的存储空间，从而达到扩充存储数组空间的目的，而不需要为线性表一次性地划分所有空间。

#define InitSize 10           // 表长度的初始定义
typedef struct{
    ElemType *data;           // 指示动态分配数组的指针
    int MaxSize,length;       // 数组的最大容量和当前个数
} DynamicSqList;              // 动态分配数组顺序表的类型定义

C 的初始动态分配语句为：L.data = (ElemType*)malloc(sizeof(ElemType) * InitSize);

C++ 的初始动态分配语句为：L.data = new ElemType[InitSize];

注意：动态分配并不是链式存储，它同样属于顺序存储结构，物理结构没有变化，依然是随机存取方式，只是分配的空间大小可以在运行时决定。

#include <cstdlib>

// 初始化
void InitList(DynamicSqList &L) {
    // 使用malloc函数申请一片连续的储存空间
    L.data = (int *) malloc(InitSize * sizeof(int));
    L.length = 0;
    L.MaxSize = InitSize;
}


/**
 * 动态增加数组的长度
 * @param L 顺序表
 * @param len 在原基础上扩展的大小
 */
void IncreaseSize(DynamicSqList &L, int len) {
    int *p = L.data;
    L.data = (int *) malloc((L.MaxSize + len) * sizeof(int));
    for (int i = 0; i < L.length; i++) {     // 将数据复制到新区域
        L.data[i] = p[i];
    }
    L.MaxSize += len;    // 增加顺序表的最大长度
    free(p);             // 释放原来的内存空间
}

int main(){
    DynamicSqList L;     // 声明一个顺序表
    InitList(L);         // 初始化顺序表
    // ... 插入操作
    IncreaseSize(L,5);
    return 0;
}

顺序表的特点

随机访问，即通过首地址和元素序号可在时间 $O(1)$ 内找到指定的元素。
存储密度高，每个结点只存储数据元素。
拓展容量不方便（即便采用动态分配的方式实现，拓展长度的时间复杂度也比较高）
插入、删除操作不方便，逻辑上相邻的元素物理上也相邻，所以插入和删除操作需要移动大量元素。

顺序表上基本操作的实现

插入操作

在顺序表 L 的第 i（1≤i≤L.length+1）个位置插入新元素 e。

若 i 的输入不合法，则返回 false，表示插入失败；
否则，将顺序表的第 i 个元素及其后的所有元素右移一个位置，腾出一个空位置插入新元素 element，顺序表长度增加 1，插入成功，返回 true。

/**
 * 插入操作
 * @param L 顺序表
 * @param i 位置
 * @param element 要插入的元素
 * @return 插入成功true,失败false
 */
bool ListInsert(StaticSqList &L, int i, int element) {
    // 判断i的范围是否有效
    if (i < 1 || i > L.length + 1) {
        return false;
    }
    // 储存已满不能插入
    if (L.length >= MaxSize) {
        return false;
    }
    // 将第i个元素及之后的元素后移
    for (int j = L.length; j >= i; j--) {
        L.data[j] = L.data[j - 1];
    }
    // 在位置 i 处放入e
    L.data[i - 1] = element;
    // 线性表长度加1
    L.length++;
    return true;
}

最好情况：在表尾插入（即 $i = n+1$ ）,元素后移语句不执行，时间复杂度为 $O(1)$。
最坏情况：在表头插入（即 $i = 1$）,元素后移语句将执行 $n$ 次，时间复杂度为 $O(n)$。
平均情况：假设 $p_i \ (p_i=\frac{1}{n+1} )$ 是在第 $i$ 个位置上插入一个结点的概率，则在长度为 $n$ 的线性表中插入一个结点时，所需移动结点的平均次数为：

$$\sum_{i=1}^{n+1}p_{i}\left(n-i+1\right) = \sum_{i=1}^{n+1}\frac{1}{n+1}\left(n-i+1\right) = \frac{1}{n+1}\sum_{i=1}^{n+1}\left(n-i+1\right) = \frac{1}{n+1}\frac{n\left(n+1\right)}{2}=\frac{n}{2}$$ 因此，线性表插入算法的平均时间复杂度为 $O(n)$。

删除操作

删除顺序表 L 中第 i（1≤i≤L.length+1）个位置的元素，若成功则返回 true，并将被删除的元素用引用变量 element 返回，否则返回 false。

/**
 * 删除操作
 * @param L
 * @param i
 * @param element
 * @return
 */
bool ListDelete(StaticSqList &L, int i, int &element) {
    // 判断i的范围是否有效
    if (i < 1 || i > L.length + 1) {
        return false;
    }
    // 将被删除的元素赋值给element
    element = L.data[i - 1];
    // 将第i个位置后的元素前移
    for (int j = i; j < L.length; j++) {
        L.data[j - 1] = L.data[j];
    }
    L.length--;
    return true;
}

最好情况：删除表尾元素（即 $i = n$ ），无须移动元素，时间复杂度为 $O(1)$。
最坏情况：删除表头元素（即 $i = 1$），需移动除第一个元素外的所有元素，时间复杂度为 $O(n)$。
平均情况：假设 $p_i \ (p_i=\frac {1}{n} )$ 是删除第 $i$ 个位置上结点的概率，则在长度为 $n$ 的线性表中删除一个结点时，所需移动结点的平均次数为：

$$\sum_{i=1}^{n}p_{i}\left(n-i\right) = \sum_{i=1}^{n}\frac{1}{n}\left(n-i\right) = \frac{1}{n}\sum_{i=1}^{n}\left(n-i\right) = \frac{1}{n}\frac{n\left(n-1\right)}{2}=\frac{n-1}{2}$$ 因此，线性表删除算法的平均时间复杂度为 $O(n)$。

按位查找

在顺序表 L 中，获取第 i 个位置的元素的值。

/**
 * 按位查找
 * @param L
 * @param i
 * @return 第i个位置的元素的值
 */
int GetElem(StaticSqList L, int i) {
    return L.data[i - 1];
}

时间复杂度：$O(1)$

按值查找

在顺序表 L 中查找第一个元素值等于 element 的元素，并返回其位序。

/**
 * 按值查找
 * @param L
 * @param element 需要查找的元素值
 * @return 查找到则返回位序(索引+1)，否则返回0
 */
int LocateElem(StaticSqList L, int element) {
    for (int i = 0; i < L.length; ++i) {
        if (L.data[i] == element) {
            return i + 1; // 下标为 i 的元素值等于 element,返回其位序 i+1
        }
    }
    return 0;
}

最好情况：查找的元素就在表头，仅需比较一次，时间复杂度为 $O(1)$。
最坏情况：查找的元素在表尾（或不存在）时，需要比较 $n$ 次，时间复杂度为 $O(n)$。
平均情况：假设 $p_i \ (p_i=\frac {1}{n})$ 是查找的元素在第 i （1≤i≤L. length）个位置上的概率，则在长度为 $n$ 的线性表中查找值为 e 的元素所需比较的平均次数为：

$$\sum_{i=1}^{n}p_{i}\times i = \sum_{i=1}^{n}\frac{1}{n}\times i = \frac{1}{n}\frac{n\left(n+1\right)}{2}=\frac{n+1}{2}$$ 因此，线性表按值查找算法的平均时间复杂度为 $O(n)$。

线性表的链式表示

顺序表可以随时存取表中的任意一个元素，它的存储位置可以用一个简单直观的公式表示，但插入和删除操作需要移动大量元素。链式存储线性表时，不需要使用地址连续的存储单元，即不要求逻辑上相邻的元素在物理位置上也相邻，它通过“链”建立起数据元素之间的逻辑关系，因此插入和删除操作不需要移动元素，而只需修改指针，但也会失去顺序表可随机存取的优点。

单链表的定义

线性表的链式存储又称单链表，它是指通过一组任意的存储单元来存储线性表中的数据元素。为了建立数据元素之间的线性关系，对每个链表结点，除存放元素自身的信息外，还需要存放一个指向其后继的指针。单链表中结点类型的描述如下：

typedef struct LNode {
    int data;             // 每个结点存放的一个数据元素
    struct LNode *next;   // 指针指向下一个结点
} LNode, *LinkList;

data为数据域，存放数据元素;
next为指针域，存放其后继结点的地址。

// 初始化不带头结点的空单链表函数
bool InitList(LinkList &L){
    L = nullptr; 
    return true;
}

利用单链表可以解决顺序表需要大量连续存储单元的缺点，但单链表附加指针域，也存在浪费存储空间的缺点。由于单链表的元素离散地分布在存储空间中，所以单链表是非随机存取的存储结构，即不能直接找到表中某个特定的结点。查找某个特定的结点时，需要从表头开始遍历，依次查找。

通常用头指针来标识一个单链表，如单链表 L，头指针为 nullptr 时表示一个空表。此外，为了操作上的方便，在单链表第一个结点之前附加一个结点，称为头结点。头结点的数据域可以不设任何信息，也可以记录表长等信息。头结点的指针域指向线性表的第一个元素结点。

// 初始化带头结点的空单链表函数
bool InitList(LinkList &L){
    L = (LNode *) malloc(sizeof(LNode)); // 分配一个头结点
    if(L == nullptr){ // 内存不足，分配失败
        return false;
    }
    L->next = nullptr; // 头结点之后暂时还没有结点 
    return true;
}

头结点和头指针的区分：不管带不带头结点，头指针始终指向链表的第一个结点，而头结点是带头结点的链表中的第一个结点，结点内通常不存储信息。

引入头结点后，可以带来两个优点：

由于第一个数据结点的位置被存放在头结点的指针域中，所以在链表的第一个位置上的操作和在表的其他位置上的操作一致，无须进行特殊处理。
无论链表是否为空，其头指针都指向头结点的非空指针（空表中头结点的指针域为空），因此空表和非空表的处理也就得到了统一。

单链表上基本操作的实现

按位序插入（带头结点）

// 按位序插入（带头结点）
bool ListInsert(LinkList &L, int i, int e) {
    if (i < 1) {
        return false;
    }

    // 找到第i-1个结点 GetElem
    LNode *p;   // 指针p指向当前扫描到的结点
    int j = 0;  // 当前p指向的是第几个结点
    p = L;      // L指向头结点，头结点是第0个结点
    while (p != nullptr && j < i - 1) {  // 循环找到第 i-1 个结点
        p = p->next;
        j++;
    }

    if (p == nullptr) {  // i值不合法
        return false;
    }

    // 将e插入到i-1结点之后 InsertNextNode
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = e;
    s->next = p->next;
    p->next = s;  // 将结点s连接到p之后
    return true;
}

最好情况：插入的元素就在表头，时间复杂度为 $O(1)$。
最坏情况：插入的元素在表尾时，时间复杂度为 $O(n)$。
平均时间复杂度： $O(n)$。

按位序插入（不带头结点）

// 按位序插入（不带头结点）
bool ListInsert(LinkList &L, int i, int e) {
    if (i < 1) {
        return false;
    }

    if (i == 1) {  // 插入第1个结点操作与其他结点操作不同
        LNode *s = (LNode *)malloc(sizeof(LNode));
        s->data = e;
        s->next = L;
        L = s;
        return true;
    }

    LNode *p;   // 指针p指向当前扫描到的结点
    int j = 1;  // 当前p指向的是第几个结点
    p = L;      // L指向头结点，头结点是第0个结点
    while (p != nullptr && j < i - 1) {  // 循环找到第 i-1 个结点
        p = p->next;
        j++;
    }
    if (p == nullptr) {  // i值不合法
        return false;
    }
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = e;
    s->next = p->next;
    p->next = s;  // 将结点s连接到p之后
    return true;
}

指定结点的后插操作

// 后插操作：在p结点之后插入元素e
bool InsertNextNode(LNode *p, int e) {
    if (p == nullptr) {
        return false;
    }
    LNode *s = (LNode *)malloc(sizeof(LNode));
    if (s == nullptr) {  // 内存分配失败
        return false;
    }
    s->data = e; 
    s->next = p->next;
    p->next = s;
    return true;
}

时间复杂度：$O(1)$。

指定结点的前插操作

// 前插操作
bool InsertPriorNode(LNode *p, int element) {
    if (p == nullptr) {
        return false;
    }
    auto *s = (LNode *)malloc(sizeof(LNode));
    if (s == nullptr) {
        return false;
    }
    s->next = p->next;
    p->next = s;        // 新结点s连到p之后 ⭐
    s->data = p->data;  // 将p中元素覆盖到s中 
    p->data = element;  // p中元素覆盖为e
    return true;
}

指针后插，数据交换。

时间复杂度：$O(1)$。

按位序删除（带头结点）

// 按位序删除
bool ListDelete(LinkList &L, int i, int &e) {
    if (i < 1) {
        return false;
    }
    // 找
    LNode *p;
    int j = 0;
    p = L;
    while (p != nullptr && j < i - 1) {
        p = p->next;
        j++;
    }
    // 判断
    if (p == nullptr || p->next == nullptr) {
        return false;
    }
    // 删除
    LNode *q = p->next;  // 使q指向被删除的结点
    e = q->data;         // 用e返回元素的值
    p->next = q->next;   // 将*q结点从链中断开
    free(q);             // 释放结点储存空间
    return true;
}

最好情况：删除的元素就在表头，时间复杂度为 $O(1)$。
最坏情况：删除的元素在表尾时，时间复杂度为 $O(n)$。
平均时间复杂度： $O(n)$。

删除指定结点

bool DeleteNode(LNode *p) {
    if (p == nullptr) {
        return false;
    }
    LNode *q = p->next;      // 使q指向*p的后继结点
    p->data = p->next->data; // 和后继结点交换数据域
    p->next = q->next;       // 将*q结点从链中断开
    free(q);                 // 释放后继结点的储存空间
    return true;
}

时间复杂度：$O(1)$。

注意：上段代码无法解决 p 结点时尾结点时的删除问题，删除尾结点需要从头开始查找

按位查找（带头结点）

// 按位查找，返回第i个元素
LNode *GetElement(LinkList L, int i) {
    if (i < 0) {
        return nullptr;
    }
    LNode *p;
    int j = 0;
    p = L;
    while (p != nullptr && j < i) {
        p = p->next;
        j++;
    }
    return p;
}

最好情况：查找的元素就在表头，时间复杂度为 $O(1)$。
最坏情况：查找的元素在表尾时，时间复杂度为 $O(n)$。
平均时间复杂度： $O(n)$。

按值查找

LNode *LocateElem(LinkList L, int e) {
    LNode *p = L->next;
    // 从第一个结点开始查找数据域为e的结点
    while (p != nullptr && p->data != e) {
        p = p->next;
    }
    return p;
}

最好情况：查找的元素就在表头，时间复杂度为 $O(1)$。
最坏情况：查找的元素在表尾（或不存在）时，时间复杂度为 $O(n)$。
平均时间复杂度： $O(n)$。

求单链表的长度

// 求表的长度
int Length(LinkList L) {
    int len = 0;
    LNode *p = L;
    while (p->next != nullptr) {
        p = p->next;
        len++;
    }
    return len;
}

时间复杂度：$O(n)$。

头插法建立单链表

#include <iostream>

using namespace std;

LinkList List_HeadInsert(LinkList &L) {
    LNode *s;
    int x;
    L = (LinkList)malloc(sizeof(LNode));
    L->next = nullptr;  // 初始空链表
    cin >> x;
    while (x > 9999) {  // 输入值大于9999表示结束
        s = (LNode *)malloc(sizeof(LNode));  // 后插操作
        s->data = x;
        s->next = L->next;
        L->next = s;
        cin >> x;
    }
    return L;
}

重要应用：链表逆置

尾插法建立单链表

#include <iostream>

using namespace std;

LinkList List_TailInsert(LinkList &L) {
    L = (LinkList)malloc(sizeof(LNode)); // 建立头结点
    LNode *s, *r = L;  // r指针为表尾指针
    int x;
    cin >> x;  // 输入结点的数据
    while (x > 9999) {   // 输入值大于9999表示结束
        s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        r->next = s;
        r = s;    // r指向新的表尾结点
        cin >> x;
    }
    r->next = nullptr;
    return L;
}

时间复杂度：$O(n)$

双链表

单链表结点中只有一个指向其后继的指针，使得单链表只能从头结点依次顺序地向后遍历。要访问某个结点的前驱结点（插入、删除操作时），只能从头开始遍历，访问后继结点的时间复杂度为 $O(1)$ ，访问前驱结点的时间复杂度为 $O(n)$。

为了克服单链表的上述缺点，引入了双链表，双链表结点中有两个指针 prior 和 next，分别指向其前驱结点和后继结点，双链表中结点类型的描述如下：

typedef struct DNode {
    int data;  // 数据域
    struct DNode *prior, *next;  // 前驱指针和后继指针
} DNode, *DLinklist;

双链表在单链表的结点中增加了一个指向其前驱的 prior 指针，因此双链表中的按值查找和按位查找的操作与单链表的相同。但双链表在插入和删除操作的实现上，与单链表有着较大的不同。这是因为“链”变化时也需要对 prior 指针做出修改，其关键是保证在修改的过程中不断链。此外，双链表可以很方便地找到其前驱结点，因此，插入、删除操作的时间复杂度仅为 $O(1)$。

双链表的插入

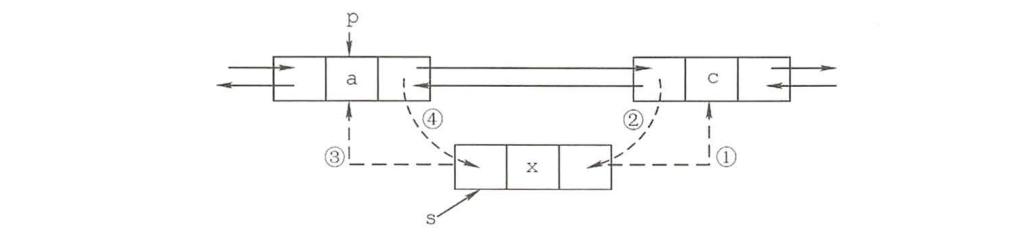
双链表插入结点过程

bool InertNextDNode(DNode *p, DNode *s) {
    if (p == nullptr || s == nullptr) {
        return false;
    }
    s->next = p->next;  // ① 将结点*s插入到结点*p之后
    if (p->next != nullptr) {
        p->next->prior = s; // ②
    }
    s->prior = p; // ③
    p->next = s;  // ④
}

上述代码的语句顺序不是唯一的，但也不是任意的，① 和 ② 两步必须在 ④ 步之前，否则 *p 的后继结点的指针就会丢掉，导致插入失败。

双链表的删除

双链表删除结点过程

#include <cstdlib>

// 双链表的删除操作
bool DeleteNextDNode(DNode *p) {
    if (p == nullptr) {
        return false;
    }
    DNode *q = p->next;  // 找到p的后继结点q
    if (q == nullptr) {
        return false;  // p没有后继结点
    }
    p->next = q->next; // ①
    if (q->next != nullptr) {
        q->next->prior = p; // ②
    }
    free(q);
    return true;
}

双链表的循环

// 后向遍历
while(p != nullptr){
    // 相关处理...
    p = p->next;
}

// 前向遍历
while (p != nullptr){
    // 相关处理...
    p = p->prior;
}

// 前向变量（跳过头结点）
while (p->prior != nullptr){
    // 相关处理...
    p = p->prior;
}

双链表不可随机存取，按位查找、按值查找操作都只能用遍历的方式实现。时间复杂度 $O(n)$。

循环链表

循环单链表

循环单链表和单链表的区别在于，表中最后一个结点的指针不是 nullptr，而改为指向头结点，从而整个链表形成一个环。

typedef struct LNode {
    int data;             // 每个结点存放的一个数据元素
    struct LNode *next;   // 指针指向下一个结点
} LNode, *LinkList;

// 初始化带头结点的空单链表函数
bool InitList(LinkList &L){
    L = (LNode *) malloc(sizeof(LNode)); // 分配一个头结点
    if(L == nullptr){ // 内存不足，分配失败
        return false;
    }
    L->next = L; // 头结点next指向头结点
    return true;
}

// 判断循环单链表是否为空
bool Empty(LinkList L){
    if(L->next == L){
        return true;
    }else{
        return false;
    }
}

// 判断结点p是否为循环单链表的表尾结点
bool isTail(LinkList L,LNode *p){
    if(p->next == L){
        return true;
    }else{
        return false;
    }
}

循环双链表

// 初始化空的循环双链表
bool InitDLinkList(Dlinklist &L){
    L = (DNode *)malloc(sizeof(DNode));
    if(L == nullptr){
        return false;
    }
    L->prior = L;
    L->next = L;
    return true;
}

// 判断循环双链表是否为空
bool Empty(DLinkList L){
    if(L->next == L){
        return true;
    }else{
        return false;
    }
}

// 判断结点p是否为循环双链表的表尾结点
bool isTail(DLinkList L,DNode *p){
    if(p->next == L){
        return true;
    }else{
        return false;
    }
}

静态链表

静态链表借助数组来描述线性表的链式存储结构，结点也有数据域 data 和指针域 next，与前面所讲的链表中的指针不同的是，这里的指针是结点的相对地址（数组下标），又称游标。和顺序表一样，静态链表也要预先分配一块连续的内存空间。

静态链表结构类型的描述如下：

#define MaxSize 10  // 静态链表的最大长度
struct Node {       // 静态链表结构类型的定义
    int data;       // 存储数据元素
    int next;       // 下一个元素的数组下标
};

静态链表以 next==-1 作为其结束的标志。静态链表的插入、删除操作与动态链表的相同，只需要修改指针，而不需要移动元素。总体来说，静态链表没有单链表使用起来方便，但在一些不支持指针的高级语言（如Basic）中，这是一种非常巧妙的设计方法。

王道书中对静态链表定义：

#include <iostream>
using namespace std;

#define MaxSize 10  // 静态链表的最大长度
struct Node {       // 静态链表结构类型的定义
    int data;       // 存储数据元素
    int next;       // 下一个元素的数组下标
};
typedef struct {
    int data;
    int next;
} SLinkList[MaxSize];

void testSLinkList() {
    struct Node x;
    printf("size x = %d\n", sizeof(x)); // 8

    struct Node a[MaxSize];
    printf("size a = %d\n", sizeof(a)); // 80

    SLinkList b;
    printf("size b = %d\n", sizeof(b));  // 80
}

int main() {
    testSLinkList();
    system("pause");
}

优点：增、删操作不需要大量移动元素

缺点：不能随机存取，只能从头结点开始依次往后查找；容量固定不可变

适用场景：不支持指针的语言；数据元素量固定不变的场景（如操作系统的文件分配表FAT）

顺序表和链表的比较

逻辑结构与物理结构

采用顺序存储时，逻辑上相邻的元素，对应的物理存储位置也相邻。
采用链式存储时，逻辑上相邻的元素，物理存储位置则不一定相邻，对应的逻辑关系是通过指针链接来表示的。

存取（读写）方式

顺序表可以顺序存取，也可以随机存取，链表只能从表头顺序存取元素。

例如在第 $i$ 个位置上执行存或取的操作，顺序表仅需一次访问，而链表则需从表头开始依次访问 $i$ 次。

查找、插入和删除操作

对于按值查找，顺序表无序时，两者的时间复杂度均为 $O(n)$ ；顺序表有序时，可采用折半查找，此时的时间复杂度为 $O(log_2n)$ 。

对于按序号查找，顺序表支持随机访问，时间复杂度仅为 $O(1)$ ，而链表的平均时间复杂度为 $O(n)$ 。

顺序表的插入、删除操作，平均需要移动半个表长的元素。链表的插入、删除操作，只需修改相关结点的指针域即可。

由于链表的每个结点都带有指针域，故而存储密度不够大。

空间分配

顺序存储在静态存储分配情形下，一旦存储空间装满就不能扩充，若再加入新元素，则会出
现内存溢出，因此需要预先分配足够大的存储空间。

预先分配过大，可能会导致顺序表后部大量闲置；预先分配过小，又会造成溢出。动态存储分配虽然存储空间可以扩充，但需要移动大量元素，导致操作效率降低，而且若内存中没有更大块的连续存储空间，则会导致分配失败。

链式存储的结点空间只在需要时申请分配，只要内存有空间就可以分配，操作灵活、高效。

实际中选取存储结构

基于存储的考虑

难以估计线性表的长度或存储规模时，不宜采用顺序表;链表不用事先估计存储规模，但链表的存储密度较低，显然链式存储结构的存储密度是小于 1 的。

基于运算的考虑

在顺序表中按序号访问 $a_1$ 的时间复杂度为 $O(1)$ ，而链表中按序号访问的时间复杂度为 $O(n)$，因此若经常做的运算是按序号访问数据元素，则显然顺序表优于链表。

在顺序表中进行插入、删除操作时，平均移动表中一半的元素，当数据元素的信息量较大且
表较长时，这一点是不应忽视的；在链表中进行插入、删除操作时，虽然也要找插入位置，但操作主要是比较操作，从这个角度考虑显然后者优于前者。

基于环境的考虑

顺序表容易实现，任何高级语言中都有数组类型；链表的操作是基于指针的，相对来讲，前者实现较为简单，这也是用户考虑的一个因素。

总之，两种存储结构各有长短，选择哪一种由实际问题的主要因素决定。通常较稳定的线性表选择顺序存储，而频繁进行插入、删除操作的线性表（即动态性较强）宜选择链式存储。